August 2003

Linn Klimax Twin Stereo Amplifier: Measurements

All amplifier measurements are performed independently by BHK Labs. Please click to learn more about how we test amplifiers there. All measurement data and graphical information displayed below are the property of SoundStage! and Schneider Publishing Inc. Reproduction in any format is not permitted.

• Measurements were made with 120V AC line voltage.
• Power output and distortion plotted with both channels driven.
• Test signal applied to unbalanced inputs unless otherwise noted.
• Gain: 27.1x, 28.7dB.
• Output noise, 8-ohm load, unbalanced input, 1k-ohm input termination: wideband 0.348mV, -78.2dBW; A weighted 0.056mV, -94.1dBW.
• Output noise, 8-ohm load, balanced input, 600-ohm input termination: wideband 0.220mV, -82.2dBW; A weighted 0.035mV, -98.2dBW.
• AC line current draw at idle: 0.67A; AC line current draw in standby: 0.27A.
• Output impedance at 50Hz: 0.08 ohms.
• This amplifier does not invert polarity.

Power output with 1kHz test signal

• 8-ohm load at 1% THD: 118W
  
  
• 4-ohm load at 1% THD: 212W

General

The Linn Klimax 500 Twin design utilizes a switching power supply, and hence allows for the attractive compact form it takes. It appears that Linn has done their homework regarding shielding and managing the potential radiation and corruption from the power-supply switching action. Although I could see some switching noise in the low-power distortion readings, it was way down there in the neighborhood of the 1mV level.

Measurements shown were made through the unbalanced inputs. Most results were essentially the same through the balanced inputs with the exception of the output noise, which was lower using the balanced inputs as the balanced gain is about 6dB lower than the unbalanced input gain. Chart 1 shows the frequency response of the amp with varying loads from an open circuit down to a 4-ohm value. This amp's output impedance is low enough to not bother with plotting the NHT dummy-speaker-load response as the variation would be only of the order of +/- 0.1dB. Chart 2 illustrates how total harmonic distortion plus noise versus power varies for 1kHz and SMPTE IM test signals and amplifier output load. As can be seen, attainable power is greater for the 4-ohm load as is usual for most power amplifiers. Total harmonic distortion plus noise as a function of frequency at several different power levels is plotted in Chart 3. In this plot, the 1W level is dominated by switching noise, which is within the 80kHz measurement bandwidth used for the chart. Damping factor versus frequency is shown in Chart 4. A spectrum of the harmonic distortion and noise residue for a 1kHz test-signal frequency, 10W output level, and 4-ohm loading is plotted in Chart 5. The amount of AC line harmonics are admirably low and there is no hum modulation of some of the signal harmonics as have been seen in quite a few other amplifiers measured.

Magenta line: open circuit
Red line: 8-ohm load
Blue line: 4-ohm load

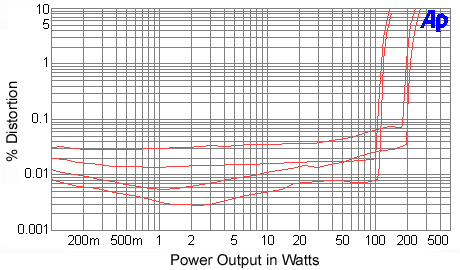
(line up at 10W to determine lines)
Top line: 4-ohm SMPTE IM
Second line: 8-ohm SMPTE IM
Third line: 4-ohm THD+N
Bottom line: 8-ohm THD+N

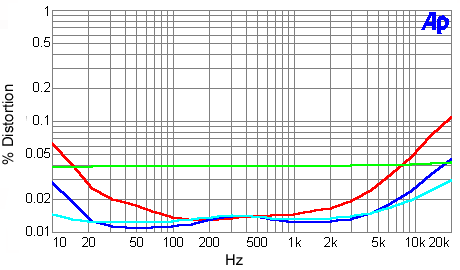
8-ohm output loading
Green line: 1W
Cyan line: 10W
Blue line: 30W
Red line: 100W

Damping factor = output impedance divided into 8

1kHz signal at 10W into an 4-ohm load

• Go Back